Notes

B Tree

6 min read

  • 완전 이진 트리의 높이가 최대 O(log(n))
    • 즉, 탐색을 안정적으로 할 수 있는 장점이 있는 자료구조
    • 그런데 이것보다 DB에서 사용하기 더 좋은 자료구조가바로
  • Balance Tree(B-Tree)
  • Binary Search Tree(BST)를 확장한 형태
    • 이진 탐색 트리를 일반화
  • 하나의 노드가 여러 개의 키를 가질 수 있는 균형트리
  • 모든 리프 노드가 동일한 레벨에 존재
  • 각 노드는 자식 노드에 대한 포인터 포함
  • 다음과 같은 특징
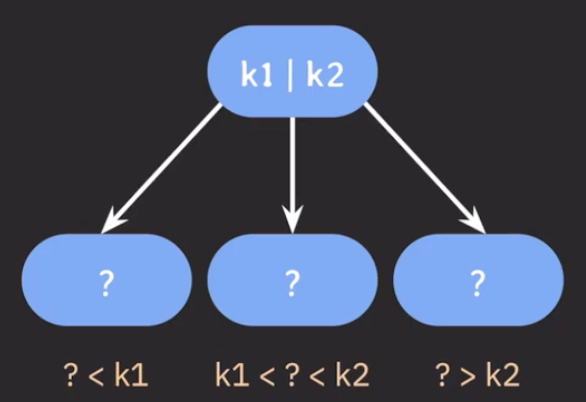
    • 다중 키 저장: 각 노드는 여러개 키 포함하며, 키들은 오름차순으로 정렬되있음
    • 자식 노드 분할: 노드의 키 개수가 N개 라면, 해당 노드는 최대 N+1 개의 자식 노드 가질 수 있음
      • 최대 M개의 자녀 가질 수 있는 B Tree를 M차 B Tree라 부름
      • 각 노드의 최대 key 수는 M-1
    • 균형 유지: 모든 리프 노드는 동일한 레벨에 위치하여 트리의 균형을 유지
    • 각 노드 최소 Key 수
      • ((올림)(M/2)-1)
  • 이진 탐색 트리에 비해 다음과 같은 장점
    • 낮은 트리 높이: 한 노드에 여러 키 저장하므로, 트리의 높이 낮아짐. 이는 탐색 시 거쳐야 하는 노드 수 줄여줌
    • 효율적인 범위 검색: 키들이 정렬되어 있어 범위 검색이 용이
    • 디스크 I/O 감소: 한 노드에 많은 키와 자식 포인터 저장하므로, 디스크 접근 횟수 줄어듬
  • 완전 이진 트리(Complete Binary Tree) 의 탐색 비용은 O(log(N))
    • 이진 탐색이 이루어 지므로 한 노드마다 최대 두갈래 분할
    • 높이 = O(log_2(N))
  • B-Tree 탐색 비용은 O(logmN)
    • 높이 = O(logmN)(m은 B-Tree 의 branching factor)
  • 삽입(추가)
    • 추가는 항상 리프 노드에 한다
    • 노드가 넘치면 가운데(median) key 기준으로 좌우 key들은 분할하고 가운데 key는 승진
      • M-1개보다 더 많은 키를 가진경우를 노드가 넘친다 표현

B + Tree!

  • B-Tree를 한층더 개선
  • InnoDB에서 인덱스 관리에 이걸 씀
  • 검색이 더 빠르고 범위 검색에 유용하다는 특징
  • 차이는 바로! 리프 노드간의 연결성이 추가된 자료구조
    • 하나의 리프 노드 위치 알면 그걸로 나머지 값도 탐색이 가능

B- B+차이

  • 메모리 효율
    • B-Tree
      • 각 노드에 데이터 주소값 뿐만 아니라 실제 데이터도 오름차순으로 정렬되어 저장
    • B+Tree
      • 리프 노드에만 실제 데이터 저장
    • 따라서, B+Tree 가 메모리 효율 측면에서 더 좋다
  • 생성 및 삭제 효율
    • B+Tree는 리프 노드 간의 연결을 나타내는 데이터도 추가로 관리해야함. 따라서, 데이터의 생성, 수정, 삭제가 일어날때 B-Tree 보다 더 많은 오버헤드 발생

왜 트리 씀? 해시 쓰면 안되나?

  • 바로 범위 검색 때문
  • 우리가 보통 수행하는 검색 패턴은 범위 검색

B Tree 계열 자료구조 시간복잡도

B+Tree, B*Tree 등 B Tree 계열은 avg case, worst case 모두 O(log n)

BST일반화 → B Tree BST는 편향될경우 O(n) 이 됨

시간복잡도가 동일한데 왜 DB Index로 B Tree가 사용되는가?

  • 내가볼땐, 한 노드에 키값이 여러개 들어갈수있어서 보조 기억 장치 히트를 덜하기때문?
  • AVL(BST) 보다 자녀를 많이 가질 수 있어서 데이터 찾을때 탐색 범위를 빠르게 좁힐 수 있다.
  • 동일 조건에서 높이가 낮다.
  • 한 노드에서 여러게의 키(뎅티ㅓ)가질 수 있음
    • 한 노드 데이터 많이가져오기에 그 노드를 불러올때 블락단위로 불러올때 한 블라의 공간활용도가 더 좋을 수 있다. 노드통째로 블락단위에 속할수있음.
  • 쉬코님!
    • B Tree index는 self-balancing BST에 비해 보조 기억 장치에 접근 적제함
    • B Tree 노드는 블록 단위의 저장 공간을 알차게 사용 가능 보조 기억 장치(secondary storage)
  • block 단위로 데이터 읽고 쓴다
    • file system이 데이터를 읽고 쓰는 논리적 단위
    • block 크기는 2의 승수로 표현
    • 대표적인 block size는 4KB, 8KB, 16KB 등
  • 단점
    • 블락단위이기에 필요한 데이터 뿐만아니라 주변의 데이터까지 읽어오는 단점 존재 성능적인 측면에서 DB에서 조회시 보조 기억 장치에 최대한 적게 접근하는게 좋다

Graph View