https://www.youtube.com/watch?v=4odNfNpMymE
TSP 알고리즘은 음이 아닌 가중치가 있는 방향성 그래프를 대상으로 한다. 음수 사이클이 생기면 무한히 이동하기 때문.
풀이법
1. 다이나믹 프로그래밍 + 비트 집합
기존에 이미 연산한 값 재사용하여 중복 계산을 줄여 실행속도를 빠르게함. 각 BIT를 하나의 도시라 생각하여 Flag로 활용한다면 도시의 방문 여부 저장 가능
2. 분기 한정
분기를 한정시켜 쓸데없는 시간 낭비 줄이는 방법. 백트래킹이 허용되는 탐색에서 더이상 탐색할 필요 없는 지점 판단.
비트 활용한 부분 집합 표현
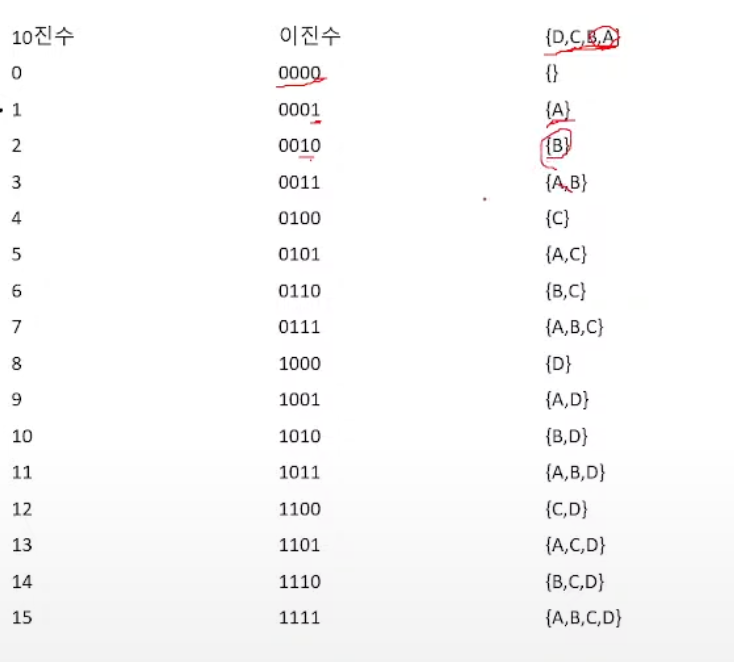
비트 마스킹
bitmasking 각 비트를 하나의 플래그로 여긴다. 자료 저장과 집합 표현을 쉽게 만든다. 예를 들어 사람에 0~31 번호가 매겨져 있고 사람 A의 친구 목록이 {0,3,6,7,10,13,28}이고, B의 친구 목록이 {0,1,4,5,6,17,21,28}일때
A, B모두 친구인 사람은? A & B = 0001 0000 0000 0000 0000 0000 0100 0001
A또는 B와 친구인 사람은? A | B = 0001 0000 0010 0010 0010 0100 1111 1011
다시 돌아와서

접근법 2: 동적 계획법(DP) + 비트마스킹 (중요!)
코딩 테스트에서 TSP 문제가 나온다면 대부분 이 방법을 요구합니다. 완전 탐색의 비효율성을 개선한 방법입니다.
핵심 아이디어:
“현재 A 도시에 있고, 지금까지 S 집합의 도시들을 방문했을 때, 앞으로 남은 도시들을 모두 방문하고 출발점으로 돌아가는 데 필요한 최소 비용”을 계산하고 저장(Memoization)합니다.
이때, “방문한 도시들의 집합 S”를 표현하기 위해 **비트마스킹(Bitmasking)**을 사용합니다.
1. 비트마스킹(Bitmasking) 이란?
정수의 이진수 표현을 집합처럼 사용하는 기법입니다.
- 도시가 N개 있을 때, N 비트(bit)짜리 정수 하나로 방문 상태를 표현합니다.
- i번째 비트가 1이면 i번 도시를 방문했다는 의미, 0이면 방문하지 않았다는 의미입니다.
예시 (N=4):
- 0001 (10진수 1): 0번 도시만 방문함
- 1001 (10진수 9): 0, 3번 도시를 방문함
- 1111 (10진수 15): 모든 도시를 방문함
Java 비트 연산:
- i번 도시 방문 처리: visited | (1 << i)
- i번 도시 방문 여부 확인: (visited & (1 << i)) != 0
- 모든 도시를 방문했는지 확인용 마스크: (1 << N) - 1
2. DP 상태 정의
dp[current][visited] = 현재 current 도시에 있고, visited 마스크에 해당하는 도시들을 방문했을 때, 나머지 도시들을 모두 방문하고 출발점으로 돌아가는 최소 비용
Java 코드 구조 예시:
public class TspDpBitmask {
static final int INF = 16 * 1_000_000; // 충분히 큰 값 (도시 수 * 최대 비용)
static int N;
static int[][] W;
static int[][] dp;
static int ALL_VISITED;
public static void main(String[] args) {
// 예시 입력
N = 4;
W = new int[][]{
{0, 10, 15, 20},
{5, 0, 9, 10},
{6, 13, 0, 12},
{8, 8, 9, 0}
};
// dp 테이블 초기화. dp[도시 수][2^도시 수]
dp = new int[N][(1 << N)];
ALL_VISITED = (1 << N) - 1; // 모든 도시를 방문했을 때의 비트마스크 (예: 1111)
// 0번 도시에서 출발
int result = tsp(0, 1 << 0); // 현재 0번 도시, 0번 도시 방문처리(0001)
System.out.println("최소 비용: " + result);
}
/**
* @param current 현재 위치한 도시
* @param visited 방문한 도시들의 집합(비트마스크)
* @return 남은 도시들을 방문하고 출발점으로 돌아가는 최소 비용
*/
public static int tsp(int current, int visited) {
// 1. 모든 도시를 방문한 경우
if (visited == ALL_VISITED) {
// 현재 도시에서 출발 도시(0)로 돌아갈 수 없다면
if (W[current][0] == 0) {
return INF; // 불가능한 경로
}
return W[current][0]; // 출발 도시로 돌아가는 비용 반환
}
// 2. 이미 계산한 값이 있다면 (메모이제이션)
if (dp[current][visited] != 0) {
return dp[current][visited];
}
// 3. 아직 계산하지 않았다면
dp[current][visited] = INF; // 우선 최댓값으로 초기화
// 다음 방문할 도시(next)를 탐색
for (int next = 0; next < N; next++) {
// next 도시를 아직 방문하지 않았고, current -> next 경로가 있다면
if ((visited & (1 << next)) == 0 && W[current][next] != 0) {
// 재귀 호출
// next 도시로 이동하고, 방문 처리를 한 후의 최소 비용 + 현재 위치에서 next로 가는 비용
int cost = tsp(next, visited | (1 << next)) + W[current][next];
// 기존의 최소 비용과 비교하여 갱신
dp[current][visited] = Math.min(dp[current][visited], cost);
}
}
return dp[current][visited];
}
}- 장점: 시간 복잡도가 O(N² * 2^N)으로, N이 약 16~20 정도까지 해결 가능합니다. N!에 비해 엄청난 개선입니다.
요약 및 학습 로드맵
| 알고리즘 | 시간 복잡도 | 해결 가능한 N의 크기 | 핵심 개념 |
| 완전 탐색 (DFS) | O(N!) | ~10 | 재귀, 백트래킹 |
| DP + 비트마스킹 | O(N² * 2^N) | ~20 | 동적 계획법, 메모이제이션, 비트마스킹 |
TSP 문제를 정복하기 위한 단계별 학습 추천:
-
1단계: 완전 탐색(DFS)으로 구현해보기
- 먼저 가장 간단한 방법으로 문제를 직접 풀어보면서 TSP 문제의 구조를 완벽하게 이해하는 것이 중요합니다.
-
2단계: 비트마스킹 개념 익히기
- Java의 비트 연산자(&, |, ^, <<, >>)에 익숙해져야 합니다. 비트마스킹을 사용하는 간단한 다른 문제들을 풀어보며 연습하는 것을 추천합니다.
-
3단계: DP + 비트마스킹으로 구현하기
-
위의 코드 예시를 보면서 DP 상태(dp[current][visited])가 무엇을 의미하는지 곱씹어보세요. 이 정의를 이해하는 것이 가장 중요합니다.
-
코드를 직접 짜보면서 재귀 함수의 종료 조건, 메모이제이션 처리, 점화식 부분을 어떻게 코드로 옮기는지 익혀야 합니다.
-
TSP는 어렵지만, 그만큼 얻어가는 것이 많은 문제입니다. 특히 DP와 비트마스킹 조합은 다른 여러 고난도 문제에서도 활용되는 강력한 테크닉이니 꼭 마스터하시길 바랍니다. 화이팅입니다