위상 정렬(Topology Sort)

1. 설명

선수과목 개념! 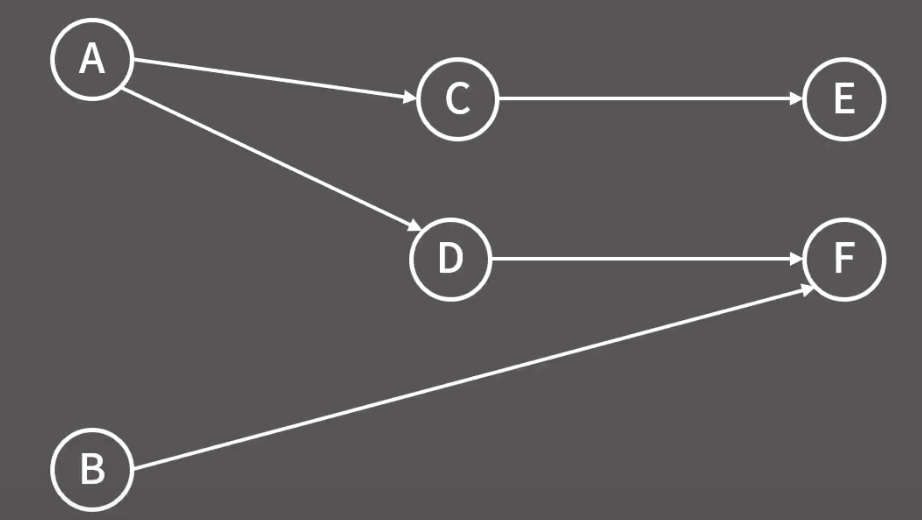위상 정렬: 방향 그래프에서 간선으로 주어진 정점 간 선후관계를 위배하지 않도록 나열하는 정렬

그래프에 사이클이 존재할 경우 올바른 위상정렬이 나올수 없다.

따라서 위상 정렬은 사이클이 존재하지 않는 방향 그래프에서만 가능한 정렬이다.

사이클이 존재하지 않는 방향 그래프를 **DAG(Directed Acyclic Graph)**라고 부른다. Acyclic이 비순환이라는 뜻인듯?

2. 구현

2.1 생각하기

위상 정렬에서 가장 먼저 올 수 있는게 무엇일지 생각해보자.

자기한테 들어오는 정점이 없어야 된다.
- indegree가 0 인 것.

indegree 가 0인것중에 임의로 A를 택한경우다. A에 연결된게 B인데 이미 A는 정렬이 되었고 B는 이제부터 자유의 몸이니 A에서 다른 정점으로 나가는 간선이 이제 의미가 없어진다.

A와 A에서 나가는 간선 모두 지우고 위상 정렬을 이어가자. 택하는건 모두 indgree가 0 인것중 임의로 택하는 것임. 임의로 해도 ㄱㅊ음.

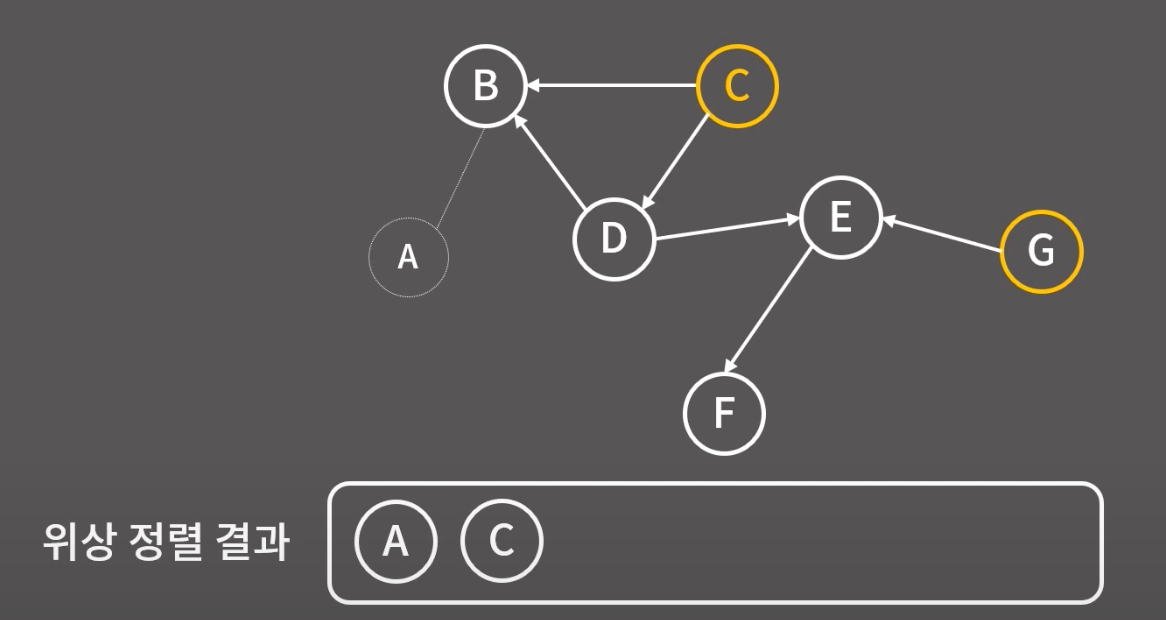
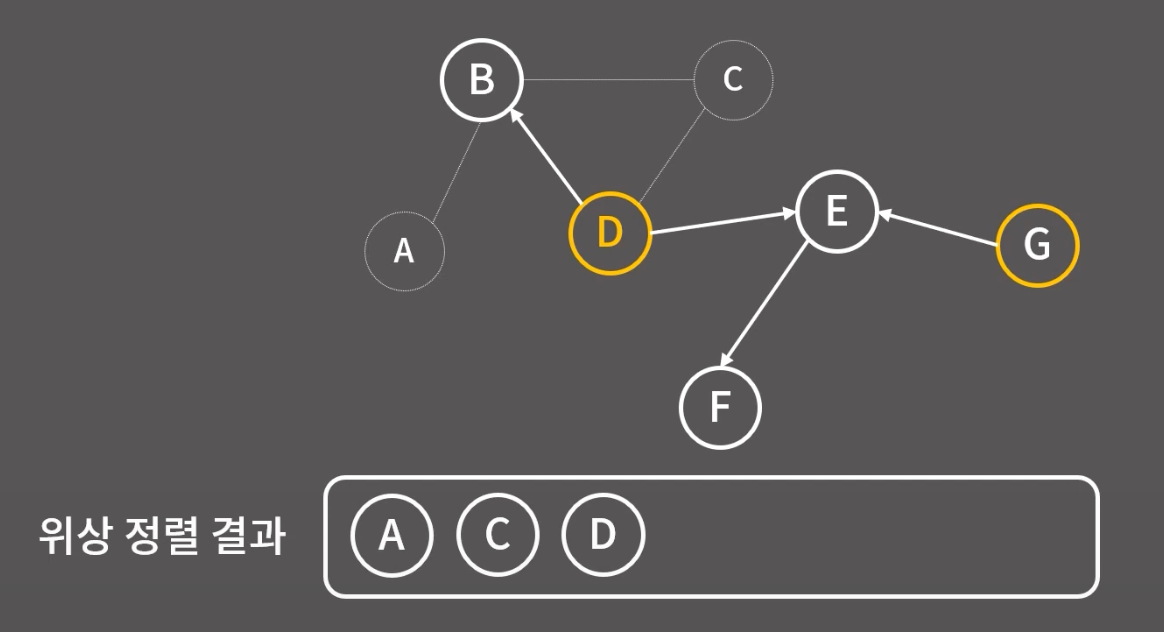
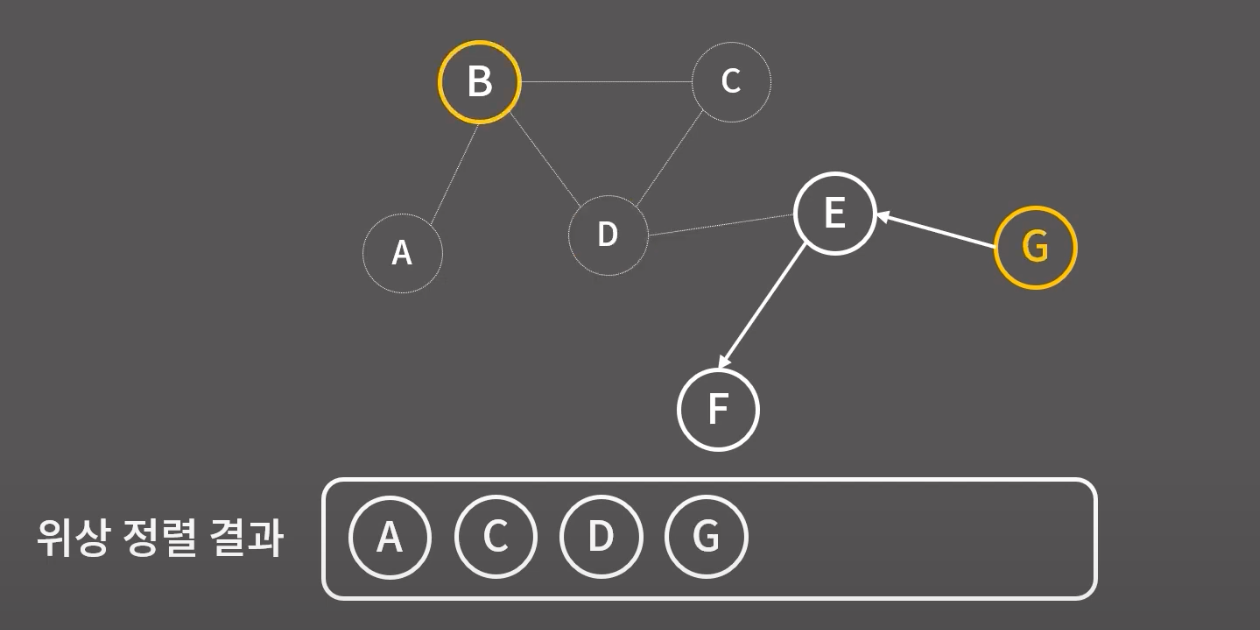
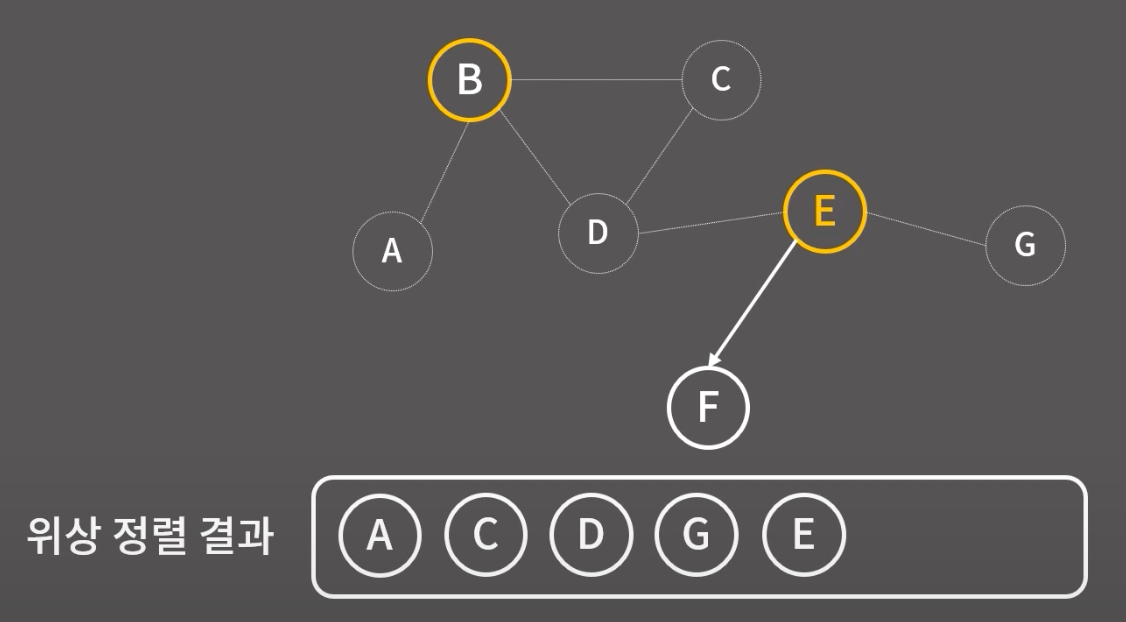
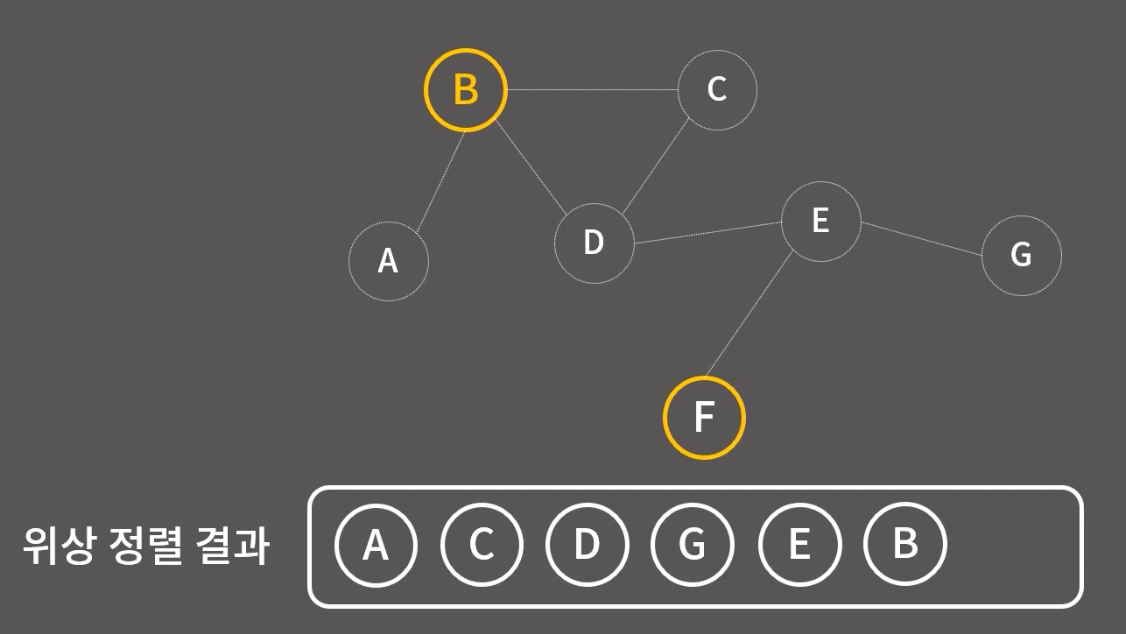
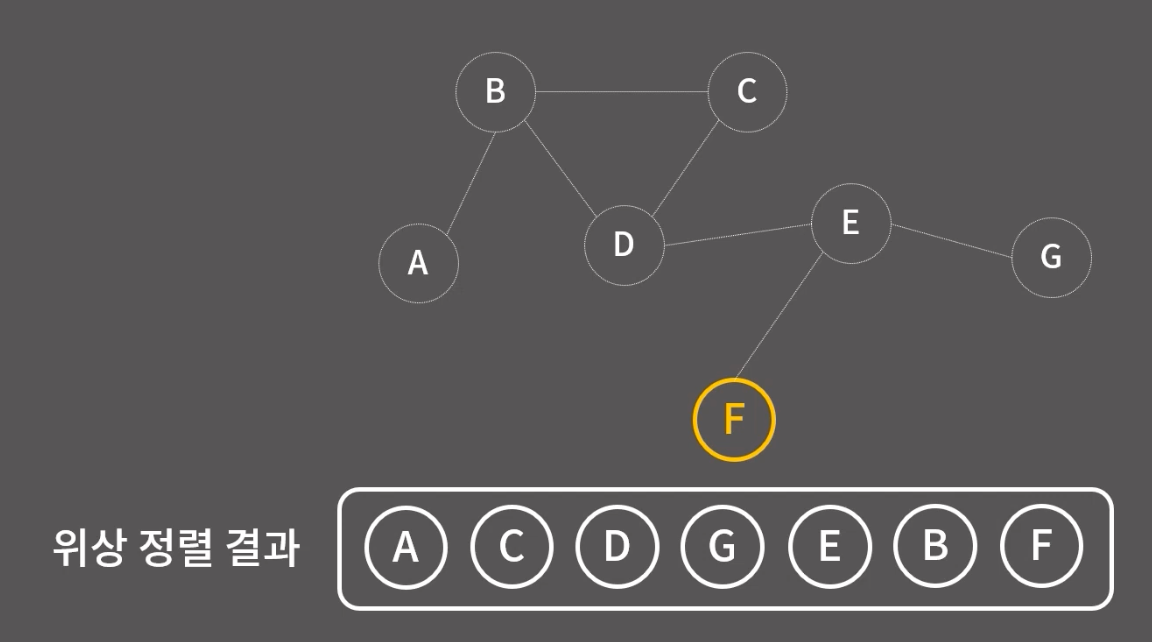위상 정렬 완료~!

2.2 코드로 구현

구현의 편의를 위한 성질
- 정점과 간선을 실제로 지울 필요 없이 미리 indgree 값을 저장했다가 매번 뻗어나가는 정점들의 indegree 값만 1만 감소시켜도 과정을 수행 가능
- indegree 가 0인 정점을 구하기 위해 매번 모든 정점 확인대신 목록을 따로 저장하고 있다가 직전에 제거한 정점에서 연결된 정점들만 추가

맨 처음 모든 간선 읽으며 indegree 테이블 채움
indegree 가 0인 정점들을 모두 큐에 넣음
큐에서 정점을 꺼내어 위상 정렬 결과에 추가
해당 정점으로부터 연결된 모든 정점의 indegree 값을 1감소시킴 이때 indegree가 0이되면 그 정점을 큐에 추가
큐가 빌 때 까지 3,4 반복

사이클이 있는 경우는 어떻게 될까

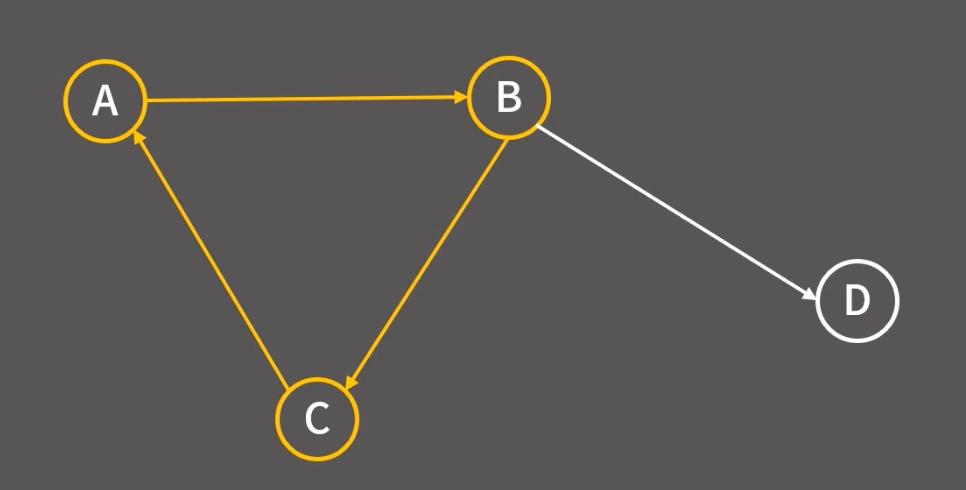A, B, C 중 어느것도 indegree가 0이 될 수 없다! 사이클에 포함되어 있는건 큐에 못들어간다. 그러므로 위상 정렬 결과에 모든 정점이 있지않은것! 이 사실로 그래프에 사이클 존재 유무 또한 판단이 가능하다

구현 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
//2252
class Main {
    static int N, M;
    static int[] indegree;
    //    static Node[] nodes;
    static List<List<Integer>> graph = new ArrayList<>();
 
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());// 학생 수 1 ~ 32000
        M = Integer.parseInt(st.nextToken());// 키를 비교한 횟수 1~100000
        indegree = new int[N + 1];
        //nodes = new Node[N + 1];
//        for (int i = 1; i <= N; i++) {
//            nodes[i] = new Node(i);
//        }
        graph.add(null);
        for (int i = 1; i <= N; i++) {
            graph.add(new ArrayList<>());
        }
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int A = Integer.parseInt(st.nextToken());
            int B = Integer.parseInt(st.nextToken());
            //A는 B의 앞에 있어야한다. A -> B
            //위상 정렬을 하기위한 조건은 DAG(Directed Acylic Graph)
            graph.get(A).add(B);
            indegree[B]++; // B로 들어가는거기 때문에 인디그리가 상승한다.
        }
        Queue<Integer> q = new ArrayDeque<>();
        for (int i = 1; i <= N; i++) {
            if (indegree[i] == 0) {
                q.add(i);
            }
        }
        StringBuilder sb = new StringBuilder();
 
        while (!q.isEmpty()) {
            int i = q.poll();
            sb.append(i + " ");
            if (graph.get(i).size() == 0) continue;
            for (int k : graph.get(i)) {
                indegree[k]--;
                if (indegree[k] == 0) {
                    q.add(k);
                }
            }
        }
        System.out.print(sb.toString());
 
    }
 
    static class Node {
        int idx;
        Node next;
 
        Node(int idx) {
            this.idx = idx;
        }
    }
}

시간 복잡도

O(V+E)

각 정점은 큐에 최대 1번 들어가고, indegree 감소 연산은 각 간선에 대해 딱 1번만 수행된다.

Notes

Explorer