https://youtu.be/4wA3bncb64E?si=iFPbTUAB9ydaf3_I
설명
- 간선을 크기의 오름차순으로 정렬하고 제일 낮은 비용의 간선 선택
- 현재 선택한 간선이 정점 u, v 를 연결하는 간선이라고 할 때 만약 u와 v가 같은 그룹이라면 아무 것도 하지 않고 넘어가지만, 다른 그룹이라면 같은 그룹으로 만들고 현재 선택한 간선을 최소 신장 트리에 추가
- 최소 신장 트리에 V-1 개의 간선을 추가했다면 과정을 종료, 그렇지 않다면 그 다음으로 비용이 작은 간선 선택한 후 2번 과정 반복 분리 집합(Union Find, Disjoint Set)활용하면 더 효율적. O(ElogE)
크루스칼 알고리즘은 유니온 파인드를 알고있다는 가정하에 프림 알고리즘보다 구현이 쉬운편.
그림으로 이해해보기

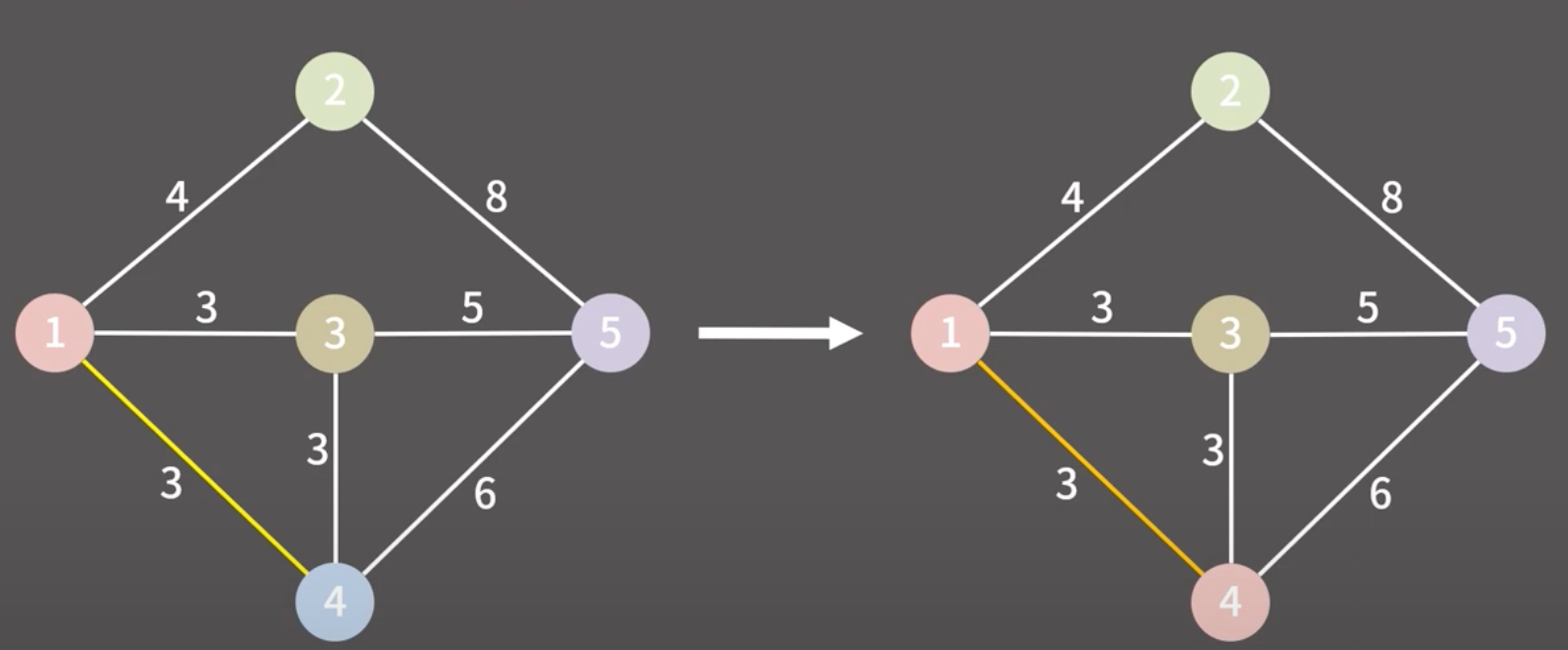
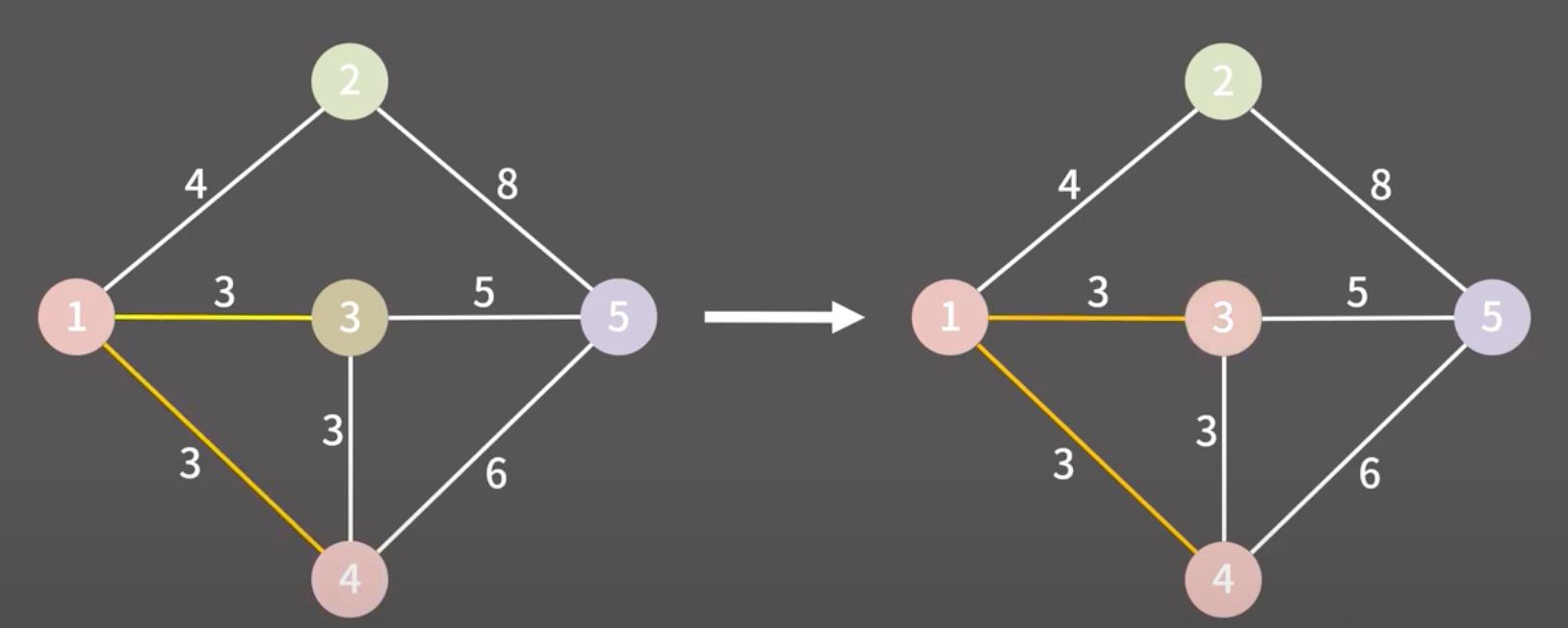
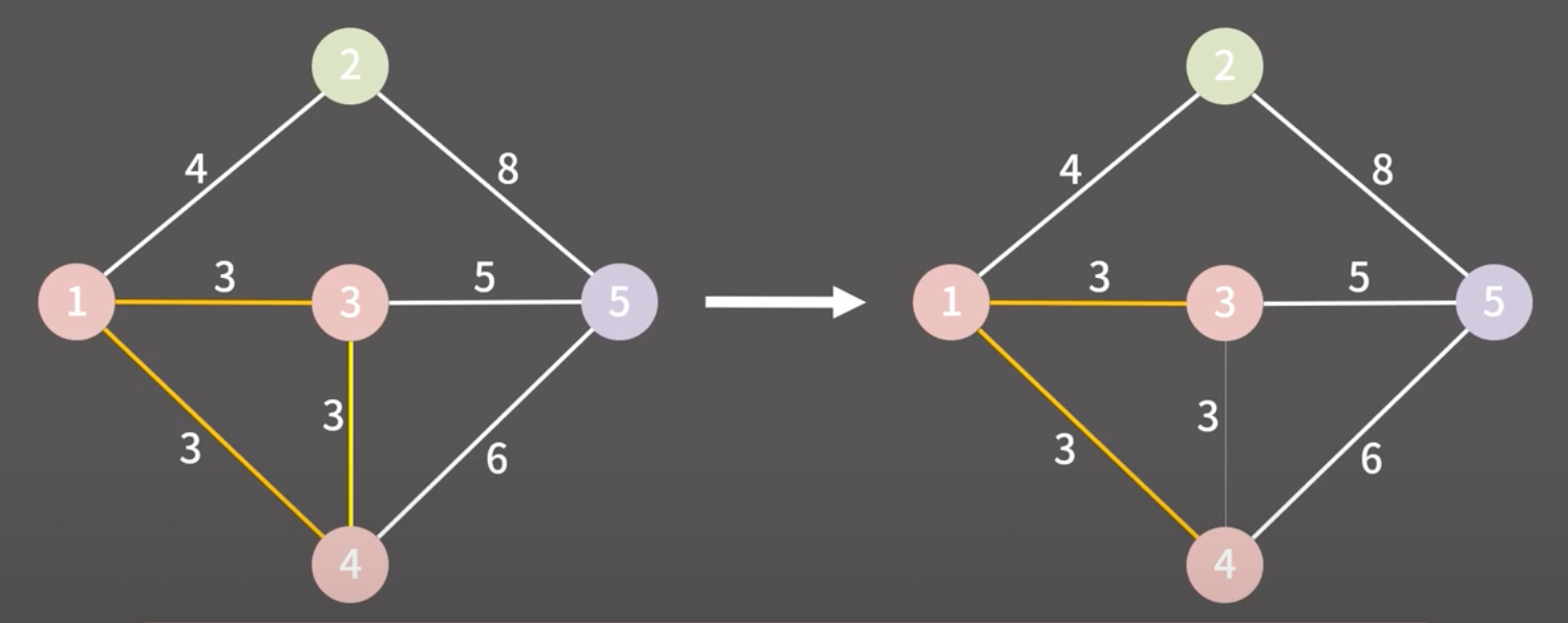 이때는 이미 그룹이 동일하기에 아무것도 안하고 다음 간선으로 가면된다!
이때는 이미 그룹이 동일하기에 아무것도 안하고 다음 간선으로 가면된다!
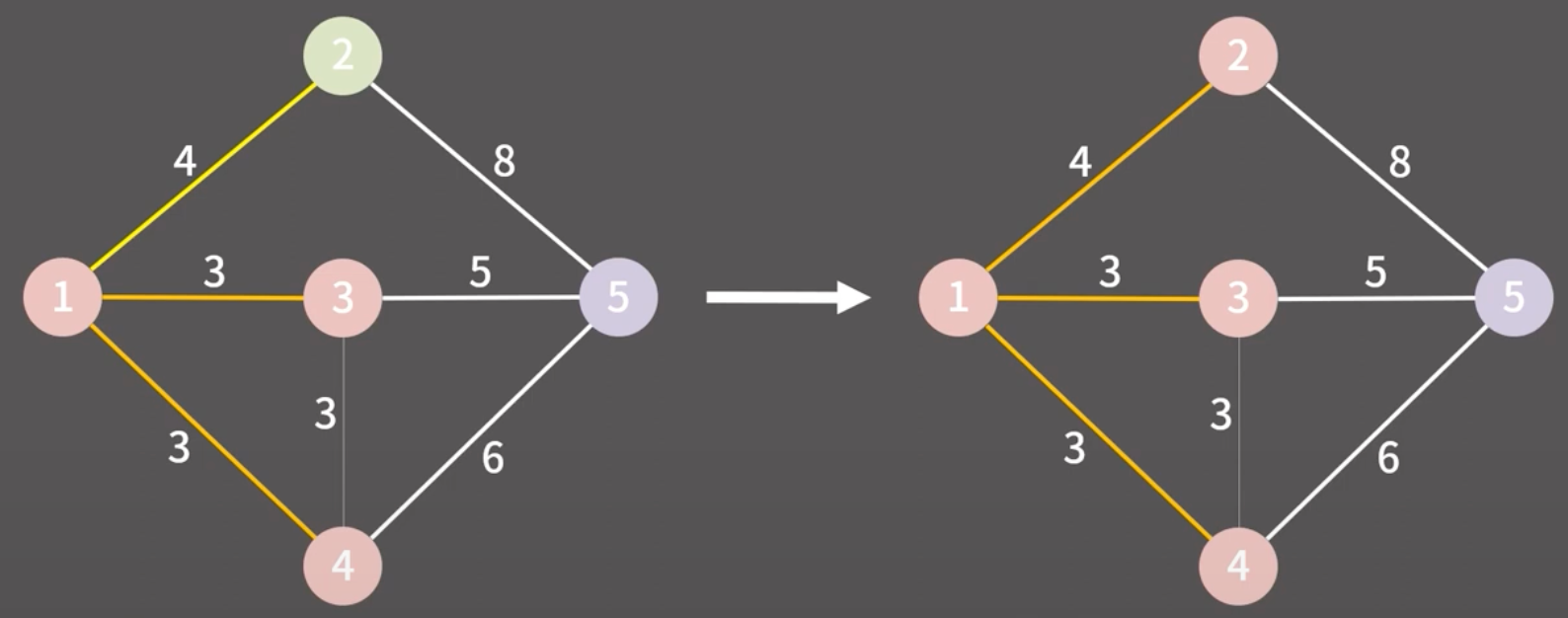 이하 생략…
이하 생략…
구현
내 생각 적어보면
- 간선 정보 얻기
- 간선 오름차숨 정렬
- 간선 정보에 연결되는 정점인덱스 있어야한다
- 이 이어진 정점들이 같은 그룹이면 다음꺼로 가고 다른 그룹이면 유니온해준다. 그리고 유니온이 된 간선은 최소신장트리에 넣는다
- 반복
- 맵 자료구조를 사용해서?
최적화에 대해서
FLood fill쓰면 O(ElogE + VE) 지만 크루스칼을 씀 O(ElogE + (상수)) == O(ElogE) 로 개선이 된다.(음 유니온 파인드 풀 최적화의 경우겠지?) amortized logN임 경로 압축 최적화만 하면! O((E+1)logE)일듯
코드
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
/**
* 크루스칼 알고리즘을 사용하여 최소 신장 트리(MST)를 찾는 자바 템플릿입니다.
*/
public class KruskalTemplate {
/**
* 간선(Edge) 정보를 저장하는 클래스
* - Comparable 인터페이스를 구현하여 가중치를 기준으로 정렬할 수 있도록 합니다.
*/
static class Edge implements Comparable<Edge> {
int src; // 시작 정점
int dest; // 도착 정점
int weight; // 가중치
public Edge(int src, int dest, int weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
// 가중치를 기준으로 오름차순 정렬
@Override
public int compareTo(Edge other) {
return this.weight - other.weight;
}
@Override
public String toString() {
return "(" + src + " - " + dest + ", w:" + weight + ")";
}
}
/**
* Union-Find (Disjoint Set) 자료구조를 위한 클래스
* - 사이클 생성 여부를 효율적으로 판별합니다.
*/
static class DisjointSet {
int[] parent;
public DisjointSet(int n) {
parent = new int[n];
// 초기에는 각 정점이 자기 자신을 부모로 가리키도록 설정 (모두 분리된 집합)
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// 특정 정점의 루트(최상위 부모)를 찾는 메서드 (경로 압축 최적화 포함)
public int find(int i) {
if (parent[i] == i) {
return i;
}
// 재귀적으로 부모를 찾아 올라가면서 경로상의 모든 노드가 루트를 직접 가리키게 함
return parent[i] = find(parent[i]);
}
// 두 정점이 속한 집합을 합치는 메서드
public void union(int i, int j) {
int rootI = find(i);
int rootJ = find(j);
// 두 정점의 루트가 다르다면, 하나의 루트를 다른 루트의 자식으로 만듦
if (rootI != rootJ) {
parent[rootI] = rootJ;
}
}
}
/**
* 크루스칼 알고리즘을 실행하여 MST를 찾는 메인 메서드
* @param V 정점의 개수
* @param edges 간선 리스트
*/
public void findMST(int V, List<Edge> edges) {
// 결과로 선택될 MST의 간선들을 저장할 리스트
List<Edge> mstEdges = new ArrayList<>();
// MST 전체 가중치
int mstWeight = 0;
// 1. 모든 간선을 가중치 기준으로 오름차순 정렬
Collections.sort(edges);
// 2. Union-Find 자료구조 초기화
DisjointSet ds = new DisjointSet(V);
// 3. 정렬된 간선을 순회하며 MST를 구성
for (Edge edge : edges) {
int rootSrc = ds.find(edge.src);
int rootDest = ds.find(edge.dest);
// 두 정점의 루트가 다르다면 (즉, 사이클을 형성하지 않는다면)
if (rootSrc != rootDest) {
// 이 간선을 MST에 추가
mstEdges.add(edge);
mstWeight += edge.weight;
// 두 집합을 하나로 합침
ds.union(edge.src, edge.dest);
// MST는 V-1개의 간선으로 구성되므로, 다 찾았다면 종료
if (mstEdges.size() == V - 1) {
break;
}
}
}
// 결과 출력
System.out.println("--- 최소 신장 트리(MST) 간선 목록 ---");
for (Edge edge : mstEdges) {
System.out.println(edge);
}
System.out.println("======================================");
System.out.println("최소 신장 트리의 총 가중치: " + mstWeight);
}
/**
* 메인 함수 (테스트용)
*/
public static void main(String[] args) {
// 정점의 개수 (0-based index, 즉 0, 1, 2, 3)
int V = 5;
// 간선 리스트 생성
List<Edge> edges = new ArrayList<>();
edges.add(new Edge(0, 1, 10));
edges.add(new Edge(0, 2, 15));
edges.add(new Edge(0, 3, 30));
edges.add(new Edge(1, 3, 40));
edges.add(new Edge(1, 4, 50));
edges.add(new Edge(2, 3, 20));
edges.add(new Edge(3, 4, 25));
/*
* 테스트 그래프 시각화 (정점 5개)
*
* (0)
* 10/ | \15
* / | \
* (1) 30 (2)
* 40\ /20 /
* (3)
* 25 \ /50
* (4)
*/
KruskalTemplate mstFinder = new KruskalTemplate();
mstFinder.findMST(V, edges);
}
}